Image 9/2018:

Opettaja Otte Heinävaara kirjoittaa taululle piirrettyyn lukujärjestykseen ”koe” sekä maanantain, keskiviikon että perjantain kohdalle. Kello on kaksitoista toukokuun 7. päivänä ja matematiikan kuusipäiväinen valmennusleiri on juuri alkanut valkeakoskelaisessa Päivölän opistossa.

Pulpeteissa istuvat yhdeksän poikaa ja yksi tyttö voisivat olla kuin mikä tahansa lukiolaisporukka. Teinit keikkuvat tuoleilla ja pureskelevat hupparinnauhaa.

”On minulla täällä viikon tarkempikin ohjelma. Haluatteko kuulla sen?” Heinävaara kysyy.

”Ei kiinnosta”, eturivin pojat mölisevät.

”Onko meillä koe yöllä?” yksi pojista kysyy sitten.

”Miten niin?” Heinävaara vastaa.

”Kun se on kirjoitettu maanantain ja tiistain väliin.”

”Se on vain suhteellisuusteorian aiheuttamaa ajan vääristymää.”

Kaikkia naurattaa.

Tässä istuu oman ikäluokkansa matematiikkahuippuja. Kuusi kertaa vuodessa Päivölään kokoontuu nuoria eri puolilta Suomea treenaamaan lukiokursseja vaativampaa matematiikkaa. Heistä parhaat pääsevät edustamaan Suomea kansainvälisiin kilpailuihin.

Täksi viikoksi opistolle on kutsuttu valmennuksissa pyörivästä muutaman kymmenen osallistujan joukosta kaikkein lupaavin kymmenikkö. Nyt maali on erityisen tärkeä: viikon päätteeksi heistä kuusi valitaan heinäkuussa pidettäviin kansainvälisiin matematiikkaolympialaisiin.

Matematiikkakilpailut eivät ole sellaista kansanhuvia kuin urheilukilpailut, mutta pohjimmiltaan matematiikassa kilpaileminen ei poikkea urheilusta.

On leirejä, kilpailua joukkueeseen pääsystä, kisamatkoja ja harjoittelua. Satoja tunteja harjoittelua. Lahjakkuuksia haalitaan valmennukseen lähettämällä kutsuja alueellisissa seitsemäsluokkalaisten sekä valtakunnallisissa peruskoululaisten ja lukiolaisten matematiikkakilpailuissa pärjänneille.

Päivölässä käyntien lisäksi osallistujien odotetaan treenaavan vapaa-ajalla. Tätä varten heille lähetetään kotitehtäviä, jotka palautetaan valmentajille.

Yksi oleellinen ero urheiluun kuitenkin on. Liikunnassa ja taiteissa tavoitteellisen harrastamisen voi aloittaa jopa alle kouluikäisenä.

Lahjakkuudet pyritään tunnistamaan varhain ja tarjoamaan motivoituneille mahdollisimman hyvät puitteet kehittyä. Matematiikassa mahdollisuudet harrastaa ohjatusti koulutuntien ulkopuolella ovat hyvin vähäiset.

Se näkyy. Suomen sijoitus matematiikkaolympialaisissa on pyörinyt viime vuosina 70:nnen tuntumassa noin sadasta osallistujamaasta. Se on huono tulos ottaen huomioon, että Suomen koulujärjestelmää pidetään yhtenä maailman parhaista. Vaikka laskevista Pisa-tuloksista on oltu viime vuosina huolissaan, suomalaiskoululaiset menestyivät viimeisimmissä matematiikkatesteissä vuonna 2015 yhä hyvin, 13:nneksi parhaiten 73 maan joukossa.

Moni miettii, koulutetaanko meillä keskivertoja huippujen kustannuksella.

Päivölän valmennusleirillä vain lyhyet ruokatauot katkaisevat aamuyhdeksästä iltayhdeksään jatkuvan opetuksen. Heinävaaran jälkeen Päivölässä käyvät muun muassa Helsingin yliopiston matematiikan dosentti Kerkko Luosto ja Åbo Akademin matematiikan tutkija Esa Vesalainen.

Kokeet kestävät vähintään neljä tuntia. Tehtäviä on kerrallaan kolme tai neljä. Esimerkiksi tällainen:

Illalla pelataan lautapelejä ja käydään kävelyllä läheisen pellon ympäri. Osa jää tekemään vielä harjoitustehtäviä.

Halsualta Keski-Pohjanmaalta tuleva Akseli Jussinmäki menee valmennuspäivinä mieluiten varhain nukkumaan.

Jussinmäki opiskelee toista vuotta Kaustisen musiikkilukion yleislinjalla. Matematiikasta hän kiinnostui jo varhain.

Ennen esikoulua hän opetteli itsekseen kertolaskemisen lahjaksi saamastaan kirjasta. Päässä laskeminen sujui erityisen helposti. Ala-asteella Jussinmäki huomasi käsittelevänsä numeroita paremmin kuin moni aikuinen.

”Isä saattoi tankattuaan kehottaa, että laskepas, kuinka paljon oli kilometrikulutus.”

Yläasteella opettaja ehdotti, että Jussinmäki voisi matematiikantunneilla jättää tehtävät väliin ja laskea itsekseen lukion kursseja.

Lukion ensimmäisellä Jussinmäki alkoi käydä Päivölässä.

”Opettaja kysyi, halusinko osallistua MAOL:n (Matemaattisten aineiden opettajien liitto) alkukilpailuun. Olin kuudes tai seitsemäs helpommassa sarjassa, niin sain kutsun valmennukseen. Ennen sitä en tiennyt mitään kisamatematiikasta.”

”Kilpailumatematiikalla” viitataan tehtävien laatuun. Ongelmat eivät ole yliopistotasoista tiedettä, vaan vaativat kilpailijoilta ennen kaikkea oivalluskykyä. Niiden on myös oltava ratkaistavissa muutamassa tunnissa.

Jussinmäki on osallistunut Itämeren alueen Baltian tie -kisaan ja pohjoismaiseen matematiikkakilpailuun. Kansainväliset mittelöt eivät ole menneet kovin hyvin, mutta valtakunnallisessa lukiolaisten matematiikkakilpailussa hän oli alkuvuonna toinen.

Matematiikassa Jussinmäkeä kiehtoo sen eksaktius.

”Jos miettii pitkään tehtävää ja saa sen ratkaistua, onhan se hieno tunne. Ja vaikka kisatehtävää ei saisi tehtyä, ratkaisu voi olla tosi hieno. Tulee tunne, ettei se olekaan yhtään vaikea, ei ole vain hoksannut.”

Sekin on kivaa, että pääsee matkustamaan.

Tänä keväänä Jussinmäki on valmistautunut kisoihin tekemällä valmennustehtäviä ja lukemalla suomalaista kilpailumatematiikan opasta, geometriaa ja valmennusmateriaaleja vähintään kymmenen tuntia viikossa.

”Hyvinä viikkoina menee varmaan kaksikymmentä, kaksikymmentäviisikin tuntia. Se vähän vaihtelee. Aina ei jaksa ja välillä pitää tehdä koulujuttuja.”

Laskemisen ohella Jussinmäki lukee, laulaa Vetelin poikakuorossa ja suunnistaa.

Lauantaina kerrotaan aakkosjärjestyksessä joukkueeseen valittujen nimet. Jussinmäki on yksi. Valinnat eivät herätä suuria tunteita, koska joukkue on helsinkiläistä Ressun lukiota käyvää Selim Virtasta lukuun ottamatta sama kuin Baltian tiessä: Jussinmäen lisäksi kuopiolainen Nerissa Shakespeare, Olli Järviniemi Kangasalta, ähtäriläinen Hermanni Huhtamäki ja espoolainen Joonatan Honkamaa.

7. heinäkuuta Suomen joukkue istuu matematiikkaolympialaisten avajaisissa Romanian toiseksi suurimmassa kaupungissa Cluj-Napocassa ja nuokkuu väsymyksestä. Joukkue on päässyt puoli neljältä aamulla hotellihuoneisiin. Herätys oli seitsemältä.

Yli 600 kilpailijaa on järjestetty valtavan Polivalentă-hallin yhdelle laidalle, toisella istuvat kutsuvieraat. Avajaisissa puhuvat muun muassa Romanian presidentti, varapresidentti ja opetusministeri. Puheissa muistutetaan, että kilpailut järjestettiin ensimmäisen kerran juuri Romaniassa vuonna 1959. Tuolloin mukana oli seitsemän maata. Tänä vuonna joukkueita on 107.

Avajaisten jälkeen kilpailijat kuljetetaan takaisin hotelliin. Poliisiautot saattavat busseja, kuten kaikkia kuljetuksia kilpailun aikana.

Suomen joukkuetta kaitsee apulaisjohtajana toimiva matematiikan jatko-opiskelija, Päivölässä opettajana toimiva Otte Heinävaara. Joukkueen johtaja on Åbo Akademissa matematiikan väitöskirjaa valmisteleva Neea Palojärvi, mutta hänet on majoitettu muualle.

Tässä vaiheessa ei enää harjoitella. Joukkue on matkustanut Romaniaan suoraan Tanskasta viikon mittaiselta kaikkien Pohjoismaiden yhteiseltä harjoitusleiriltä. Kesäkuussa joukkue treenasi yhdessä viikon Turussa. (Sinne Jussinmäki ei päässyt, koska oli vetämässä rippileiriä. ”Poikaisosia on vähänlaisesti, niin lupauduin sitten.”)

Jos joukkueella on paineita, ne eivät ainakaan näy päälle. He kiusoittelevat Heinävaaraa minkä ehtivät.

”Suomi ei ole pärjännyt viime vuosina kovin hyvin, sikäli ei ole paineita. Sitten on sekin, että ensi vuonna voi vielä osallistua”, Jussinmäki sanoo.

”Olen tyytyväinen jo siihen, että pääsin osallistumaan. Sekin on hyvä lisä CV:hen. Ehkä Ollilla on paineita. Hän on harjoitellut niin paljon”, miettii Selim Virtanen.

Olli Järviniemen tavoite on hopea. Sitä varten hän on treenannut noin kolme tuntia päivässä. Järviniemi on joukkueesta selvästi se, jolta voi odottaa eniten. Kun muita kilpailijoita askarruttaa jokin, usein he kääntyvät juuri Ollin puoleen.

Järviniemen kilpailu-ura alkoi, kun hän oli kahdeksannella luokalla peruskoululaisten matematiikkakilpailun paras suomalainen. Vain joitain kilpailuun kutsuttuja virolaisia hän ei voittanut.

Seuraavana kesänä Järviniemi osallistui Päivölän opiston kesäkurssille, jossa lasketaan neljässä viikossa lukion pitkän matematiikan kursseista seitsemän.

”Se antoi huikeasti lisää näkökulmaa.”

Yhdeksännellä luokalla Järviniemi oli lukiolaisten kilpailussa toinen ja samana kesänä hän matkusti matematiikkaolympialaisiin Rio de Janeiroon.

”Pääsin joukkueeseen tietääkseni nuorimpana suomalaisena koskaan.”

Viime syksynä Järviniemi aloitti Päivölän opiston matematiikkalinjalla, jolla lukio suoritetaan sisäoppilaitosmaisissa oloissa kahdessa vuodessa. Joukkueesta Nerissa Shakespeare käy myös Päivölää.

Järviniemelle kilpaileminen on yksi tapa haastaa itseä ja muita.

”Kilpailuissa tapaa myös samanhenkistä porukkaa Suomessa ja ulkomailla.”

Matematiikan ohella Järviniemi kilpailee tietotekniikassa. Useassa lajissa kilpaileminen on valmennettavien keskuudessa varsin tavallista. Joonatan Honkamaa matkustaa heinäkuussa kemian olympialaisiin. Hermanni Huhtamäki kilpailee bridgessä.

Kilpailupaikalle pääsevät vain kilpailijat ja valvojat. Se tuo mieleen jättimäiset ylioppilaskirjoitukset. Hallissa seisoo suorissa riveissä yli kuusisataa pulpettia. Niiden päällä odottavat nimikoidut kansiot, joissa on vastaus- ja suttupapereita, ohjeita sekä värikkäitä kortteja, joilla voi kilpailun aikana viestiä valvojien kanssa. Jos esimerkiksi haluaa vettä, pitää nostaa vesikortti ilmaan.

Kilpailijat ovat saaneet etukäteen läpinäkyvät muovipussit, johon pitää mahtua kaikki mukaan otettava. Säännöt kertovat pikkutarkasti, mitä mukana saa ja ei saa olla. Esimerkiksi kulma-asteikkoja sisältävät viivaimet ovat kiellettyjä, pienet talismanit sallittuja.

Kilpailijat saavat ensin liikkua vapaasti, viimeinen puoli tuntia on istuttava omalla paikalla. Jutella saisi, mutta harva tekee niin.

Kello 9.30 saa avata tehtävät sisältävän kirjekuoren.

Olympialaisissa lasketaan kahtena peräkkäisenä päivänä neljä ja puoli tuntia. Tehtäviä on kunakin päivänä kolme ja ne ovat vaikeusjärjestyksessä. Helpoimpia ovat tehtävät 1 ja 4. Tehtävien 3 ja 6 ratkaisemiseen yltää usein vain muutama kilpailija.

Pisteitä saa enintään seitsemän kustakin tehtävästä. Osittaisestakin ratkaisusta voidaan antaa jotakin. Toisaalta oikea vastaus ei tuo täysiä pisteitä, jos ratkaisussa on virheitä.

Hieman alle puolet osallistujista palkitaan mitalilla, jotka jaetaan suhteessa 1:2:3. Kultamitalin saa noin joka kahdestoista osallistujia. Hopeamitalisteja on kaksi kertaa ja pronssimitalisteja kolme kertaa niin paljon kuin kultaa voittaneita. Lisäksi jokainen mitalitta jäänyt mutta vähintään yhdestä tehtävästä täydet pisteet saavuttanut saa kunniamaininnan.

Suomeen on tullut kultaa kerran. Sen voitti Helsingin yliopistossa dosenttina toimiva Taneli Huuskonen vuonna 1981.

Åbo Akademin matematiikan lehtori Anne-Maria Ernvall-Hytönen kuuluu valmennuksesta vastaavaan Suomen matemaattisen yhdistyksen (SMY) valmennusjaostoon ja on sen kolmihenkisen johtoryhmän jäsen. Jaostoon kuuluu viitisentoista valmentajaa, joista moni on yliopistossa matematiikkaa tutkiva entinen kilpailija.

Ernvall-Hytönen huomauttaa haastattelussa Helsingissä, että Suomen pärjääminen olympialaisissa on linjassa muiden Pohjoismaiden kanssa lukuun ottamatta Ruotsia, joka on pärjännyt paremmin. (Pisa-tulokset ovat Ruotsissa huomattavasti Suomea heikommat.)

Sitten hän listaa heikolta vaikuttavaan menestykseen kolme syytä. Yksi on maan koko. Menestysjoukkueen saa helpommin kasaan, kun ikäluokat lasketaan sadoissa-, eikä kymmenissätuhansissa.

Toinen syy liittyy koulujen opetussuunnitelmaan. Koska olympialaiset alkoivat Itä-Euroopassa, tehtävissä näkyy yhä, mitä tuolloin on pidetty sikäläisissä kouluissa tärkeänä.

”Suomessa painotetaan vahvasti differentiaali- ja integraalilaskentaa, mikä on mielestäni fiksua, koska niillä on paljon käytännön sovelluksia. Kilpailuissa tärkeää on esimerkiksi klassinen geometria, mitä opetetaan Suomessa vähän ja mille ei juuri ole käyttöä käytännössä.”

Kolmanneksi menestykseen vaikuttavat resurssit. Valmentajille toiminta on vapaaehtoistyötä, jota he tekevät vapaa-aikansa ja perhe-elämänsä ohessa. Monessa suuremmassa maassa toimintaa pyörittää organisaatio, jossa on palkattua henkilökuntaa.

Jos ryhdyttäisiin tavoittelemaan parempaa menestystä, mitä se vaatisi? Onhan Suomessa onnistuttu saavuttamaan hyvä kansainvälinen taso esimerkiksi klassisessa musiikissa, vaikka väestöä on vähän.

”Meidän pitäisi tavoittaa kilpailijat nuorempina”, Ernvall-Hytönen vastaa.

Nyt useimmat aloittavat valmennuksen vasta lukioikäisinä. Tiedon toiminnasta pitäisi ylipäätään tavoittaa ikäluokat laajemmin. Näin tapahtuisi, jos koulujen osallistuminen kilpailuihin olisi systemaattisempaa. Tällä hetkellä mukana oleminen on opettajasta kiinni.

Ernvall-Hytönen myös uskoo, että tulokset paranisivat, jos valmennukseen osallistuisi enemmän tyttöjä.

”Tytöillä ja pojilla on yhtäläiset valmiudet oppia matematiikkaa. Tyttöjen vähäisyys tarkoittaa, että menetämme puolet ikäluokista.”

Heidän määräänsä yritetään kasvattaa esimerkiksi vuosittain pidettävillä Euroopan tyttöjen matematiikkaolympialaisilla.

”Ne ovat olemassa juuri siksi, että osallistujat näkisivät, etteivät he ole ainoita matematiikassa kilpailevia tyttöjä.”

Lisäksi Ernvall-Hytönen toivoisi, että toiminnan rahoitus tulisi kokonaan opetushallitukselta. Tällä hetkellä kuluja katetaan ministeriön tuen lisäksi apurahoilla. Hakemusten tekemiseen ja epävarmuudessa elämiseen menee energiaa ja resursseja.

”Kyllä tuloksia väistämättä parantaisi, jos pystyisimme keskittymään vain valmennukseen.”

Ernvall-Hytönen muistuttaa, että puhutaan varsin pienistä summista.

”Se, mitä tähän panostetaan, tulee moninkertaisesti takaisin.”

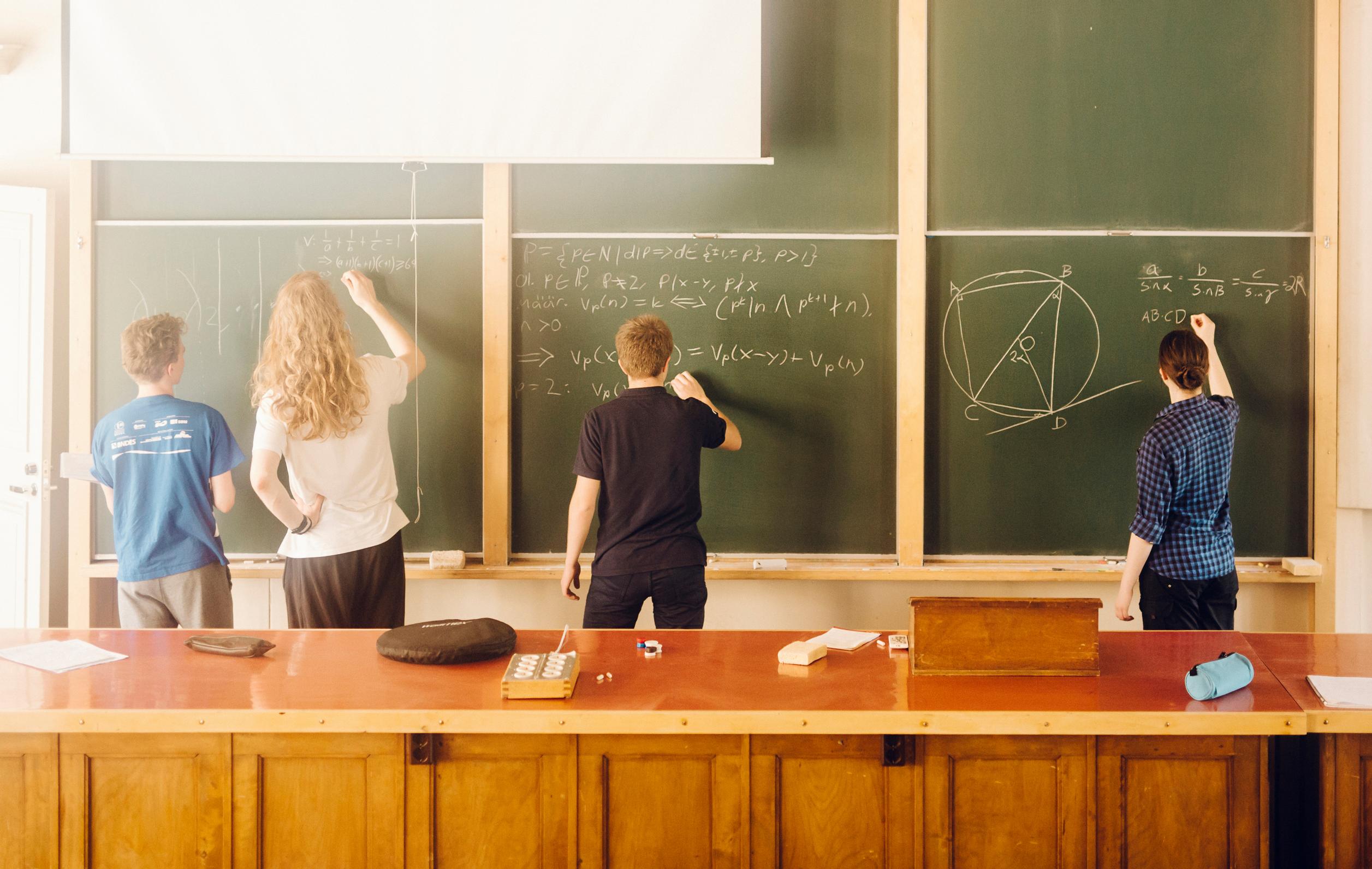
Valmennusjaostossa toiminnan tavoitteeksi ei ole asetettu vain kisamenestystä, vaan tärkeintä on ylläpitää niiden nuorten kiinnostusta matematiikkaan, joille koulun kurssit ovat liian helppoja.

Osallistujien osaamista pyritään kasvattamaan myös kilpailumatematiikkaa laajemmin siten, että he saavat hyvän pohjan jatko-opintoihin. Toiminnan toivotaan tuottavan huippuosaajia yliopistoihin ja elinkeinoelämään. Entisten kilpailijoiden joukossa onkin monia kansainvälisesti merkittävää uraa tehneitä matemaatikkoja kuten Eero Saksman ja Kaisa Matomäki.

Menestyvissä maissa kilpaileminen tarkoittaa usein paljon mittavampaa sitoutumista kuin Suomessa. Venäjän joukkueen mukana matkustava Mikhail Grigorey arvioi, että sikäläiset huiput viettävät puolet vuodesta kisamatkoilla ja leireillä. Venäjällä pelkkä karsintaprosessiin kuuluva kesäleiri, johon kutsutaan viitisenkymmentä kansallisissa kilpailuissa parhaiten menestynyttä, kestää kuukauden.

Ehkä paljon aikaa vaativa valmennus istuisi huonosti suomalaiseen ajatteluun, jossa jokaiselle nuorelle pyritään takaamaan laaja yleissivistys.

Tanskan joukkueen apulaisjohtaja Fredrik Ravn Klausen kertoo kilpailijasta, joka voitti taannoin kultaa. Se herätti Tanskassa paljon huomiota, mutta menestyksen hinta oli kova. Nuori hädin tuskin läpäisi lukion, koska vuodet olivat menneet laskiessa. Lukion jälkeen hän tosin eteni viidessä vuodessa tohtoriksi.

Kun kilpailijoita alkaa purkautua hallin ovista, odottelijat puhkeavat aplodeihin. Täällä ei nähdä samanlaisia tunteenpurkauksia kuin urheilukentillä. Ei tuuletuksia, ei kyyneleitä, ilmeet ovat lähinnä pöllämystyneitä tai väsyneitä.

”Saitko ykkösen?” suomalaiset kysyvät ensimmäisenä toisiltaan, kun he ilmestyvät yksi kerrallaan hallin ovista.

Suurin osa joukkueesta on päässyt ratkaisuun ensimmäisessä tehtävässä. Jotkut ovat kirjoittaneet toiseen ainakin jotakin. Se on ihan hyvä tulos.

Kilpailussa ajalla on iso merkitys. Heinävaaran mukaan tehtävissä ei ole mitään ylittämättömän vaikeaa. Jos aikaa olisi rajattomasti, suomalaiset kyllä löytäisivät ennen pitkää ratkaisun toisiksi vaikeimpiin, jotkut ehkä myös vaikeimpiin.

Myöhäisen lounaan jälkeen joukkue vaikuttaa lopen uupuneelta, vaikka koko päivä on istuttu paikoillaan. Shakespeare ja Järviniemi jäävät hotellille lepäämään, kun muu joukkue lähtee katsomaan nähtävyyksiä.

Kuopiolainen Nerissa Shakespeare sai edetä peruskoulun matematiikassa omaan tahtiin ja hän laski viidennellä luokalla seitsemännen luokan kirjan läpi. Yläasteella sooloilua ei enää katsottu hyvällä. Shakespeare joutui palaveriin vanhempiensa, matematiikanopettajan ja rehtorin kanssa ennen kuin lupa itseopiskeluun heltisi.

Shakespeare koki ala-asteella, että matematiikassa – niin kuin muissakin aineissa – opetus eteni hitaimpien mukaan.

”Nopeimmat joutuivat odottamaan, joten he eivät tehneet parastaan.”

Lahjakkaimpien huomioiminen on Shakespearen mielestä hyvin paljon kiinni opettajasta. Ala-asteen opettajilla ei kuitenkaan aina ole itsellään kovin laajat tiedot matematiikasta eikä välttämättä motivaatiotakaan ohjata lahjakkaimpia.

Jussinmäki on joskus miettinyt, menivätkö ensimmäiset vuodet koulussa vähän hukkaan, kun hän osasi opetetut asiat jo esikoulussa. Ja kun hän myöhemmin eteni muita nopeammin, seuraavina lukukausina hän saattoi joutua käymään uudestaan läpi tehtäviä, jotka oli jo aiemmin tehnyt.

”Olisi hyvä olla systeemi, jolla tunnistettaisiin erityislahjakkaita samalla tavalla kuin tunnistetaan niitä, jotka tarvitsevat apua enemmän.”

Tästä on tutkimustakin: kasvatustieteiden professori Kirsi Tirrin mukaan Suomessa resursseja on käytetty hyvin oppimisvaikeuksien tunnistamiseen, mutta lahjakkaiden tunnistamisessa opettajat eivät ole yhtä hyviä.

Järviniemen mielestä riittäisi, ettei huippulahjakkaita pakotettaisi käyttämään aikaansa samaan kuin muut.

”Monesti huippulahjakas on taidokkaampi kuin opettaja ja tietää itse paremmin, mitä haluaa tehdä.”

Shakespeare on osittain eri mieltä. Lahjakkaatkin kaipaavat opetusta.

”Ongelmanratkaisutaitojen oppiminen vaatii vuorovaikutusta. Matemaattista ajattelua ei voi oppia ilman opettajan ohjausta.”

Anne-Maria Ernvall-Hytösen mielestä tärkeintä olisi, että lahjakkaille annettaisiin mielekästä tekemistä, joka haastaa heitä ajattelemaan. Jos opettajalla ei ole sopivia tehtäviä omasta takaa, niitä saa valmennusjaostolta.

Uudessa opetussuunnitelmassa erityislahjakkaat yritetään huomioida paremmin painottamalla, että opetusta on eriytettävä oppilaan tason mukaan. Se on iso haaste opettajille.

Toisena kilpailupäivänä hallin ulkopuolella kilpailijoita odottelee myös yhdysvaltalaisen huippuyliopiston Massachusetts Institute of Technologyn (MIT) opiskelijavalintaa johtava Matthew McGann. Kilpailijat kiinnostavat MIT:tä ja siksi McGann on täällä kertomassa yliopiston opiskelumahdollisuuksista.

McGann vakuuttaa, että MIT on kiinnostunut yhtä lailla kultamitalisteista kuin heikommin menestyneistä.

”Tiedostamme, että mailla on hyvin erilaiset resurssit valmentaa osallistujia.”

Tämän vuoden kilpailijoista 14 on jo hyväksytty MIT:hen. Heistä neljä on Yhdysvaltojen kilpailijoita, muut tulevat muun muassa Ruotsin, Makedonian, Syyrian ja Ghanan joukkueista. Tänä syksynä opinnot aloittavissa on myös edellisvuosien kilpailijoita. McGann muistelee suomalaisiakin pääsevän MIT:hen aina silloin tällöin.

Varsinkin köyhemmissä maissa stipendi ulkomaiseen yliopistoon on houkutteleva mahdollisuus. Hondurasin joukkueen apulaisjohtaja Edgar Vásquez Alberto kertoo toivovansa, että olympialaiset avaisivat osallistujille ovia yliopistoon esimerkiksi Meksikossa tai Brasiliassa.

Kilpailumenestys voi vaikuttaa opiskelumahdollisuuksiin myös kotimaassa. Esimerkiksi Virossa mitali takaa pääsyn yliopistoon silloinkin, kun arvosana jossain muussa aineessa estäisi sen. Joissain maissa mitalistit palkitaan stipendein.

Unkarissa kymmenen parasta kansallisissa matematiikkakilpailuissa menestynyttä saa ensimmäiseksi opiskeluvuodeksi apurahan. Lisäksi heille palkataan henkilökohtainen professoritason tuutori, jonka he tapaavat säännöllisesti.

Kun Otte Heinävaara voitti olympialaisissa hopeaa vuosina 2012 ja 2013, hän sai yrityksiltä yhteydenottoja, joissa ehdotettiin tapaamista. Muun muassa Googlelta. Jotkut yhteydenotoista tosin saattoivat liittyä tietotekniikkakilpailuihin, joissa Heinävaara myös kävi.

Kello kahdelta kilpailu päättyy. Suomen joukkue päättää kävellä hotellille. He keskustelevat kolmannesta tehtävästä, joka oli kaikkein vaikein.

”Sehän oli avoin ongelma vielä 70-luvulla”, Joonatan Honkamaa huomauttaa.

Kilpailijoiden joukossa on jo kiertänyt huhuja kilpailijoista, jotka ovat päässeet lopputulokseen. Kiinalainen kilpailija on kertonut Facebookissa ratkaisseensa kolmosen.

Joukkue laskee, että ainakin kaksi mitalia tulee. Ehkä enemmänkin.

Vaikka mitaleja ei tulisi, joukkue on saanut kilpailemisesta paljon. Monelle matematiikkavalmennus on ainoa paikka, jossa pääsee kehittymään oman tasoisessaan seurassa.

Hermanni Huhtamäki toteaa, että ilman kilpailutoimintaa matematiikan harrastaminen olisi vaikeaa, koska kotipaikkakunnalla Ähtärissä siihen ei ole mahdollisuuksia. Koulun matematiikantunneilla hän ei käy, koska suoritti lukion kurssit jo peruskoulussa. Järjestely oli mahdollinen, koska isä on matematiikanopettaja.

Ehkä kilpailutoiminnan tärkein merkitys on se, että valmennettavat tapaavat toisiaan. Tätä Kirsi Tirrikin on pitänyt esillä. Lahjakkaiden pitäisi päästä välillä samanhenkiseen seuraan, jossa heillä on mahdollisuus toimia samoista asioista kiinnostuneiden kanssa. Usein lahjakkaat päätyvät koulussa auttajan rooliin. He saattavat myös peitellä osaamistaan kiusaamisen pelossa.

Vuosina 1999, 2000 ja 2001 olympialaisissa kilpaillut ja yhden pronssin saavuttanut Ernvall-Hytönen toteaa, että hänen nykyinen ystäväpiirinsä koostuu enimmäkseen entisistä valmennettavista. Aviomieskin on entinen kilpailija.

Maunulan yhteiskoulun ja Helsingin matematiikkalukion linjanjohtaja Ville Tilvis huomauttaa, että matematiikassa kilpailemisen kulttuuri on Suomessa paljon ohuempi kuin monessa muussa maassa.

”Meillä on erittäin taitavia valmentajia valtakunnan tasolla, vaikka se on vapaaehtoisorganisaatio ja liian huonosti resursoitu, mutta harrastajapohja on hyvin pieni. Vakavasti matematiikkaa harrastava voi olla koulunsa ainoa.”

Tilvis vetää tänä syksynä Maunulan lukiossa alkanutta seitsenvuotista opetus- ja kulttuuriministeriön rahoittamaa hanketta, joka pyrkii kehittämään matematiikan opetusta ennen kaikkea siihen kunnianhimoisesti suhtautuvien lukiolaisten kohdalla.

Yksi tavoitteista on luoda yhteisöä eri kouluissa opiskelevien harrastajien keskuuteen ja kehittää toimintaa paikallisella tasolla. Käytännössä se tarkoittaisi esimerkiksi kerhoja, tarvittaessa videolinkin kautta. Projektissa valmistellaan materiaalipankkia, joka sisältäisi itseopiskelutehtäviä sekä jonkinlaisen valmiin kerhokonseptin, joka opettajan olisi helppo ottaa käyttöön.

”Tietysti kerho vaatii jonkun, joka sitä pitää, eikä Suomessa ole isoja resursseja tämän kaltaisen toiminnan pyörittämiseen.”

Vaikka Maunulan lukion hanke on suunnattu ennen kaikkea lukioikäisille, Tilvis toivoo sen aktivoivan myös peruskoululaisia.

”Yläkouluikäisillä olisi aikaa. Jos saataisiin aikaan yläkoululaisia vetäviä kerhoja, lukioon tullessa he olisivat jo valmiita matematiikan harrastajia.”

Akseli Jussinmäki myöntää, että matematiikan harrastaminen tuntuu joskus yksinäiseltä.

”Olisi kiva jutella siitä jonkun toisen kanssa.”

Nyt se on mahdollista sosiaalisessa mediassa. Valmennettavilla on oma Telegram-ryhmä, jossa keskustellaan matematiikasta.

”Mutta kyllä muustakin”, Jussinmäki kertoo.

Heinäkuussa viestiteltiin:

”Haluuko ihmiset kuulla hauskan pelin?”

”Jos se on oikeesti hauska.”

”Öö no, riippuu näkökannasta, aika basic. Siis siinä on yksinkertaset säännöt: annetaan luvut n ja m ja kaks ihmistä lisää vuorotellen nollasta alkavaan summaan joko n:n tai m:n. Tavotteena on saada joku k, joka annetaan myös, jos menee k:n yli, niin häviää ja jos saa k:n niin voittaa. Luonnollisesti jos vastapelaaja saa k:n niin häviää.”

”Eli siis: sä häviät pelin jos ja vain jos sun vuoron jälkeen luku on > k?”

”No kai sen noinki voi ajatella.”

”Toi on hutunkeiton yleisen tapauksen erikoistapaus, jota en oo ratkassu.”

Olympialaisten lopuksi on päättäjäiset. Polivalentăssa kuullaan taas vaikuttavaa joukkoa Romanian eturivin poliitikoita ja palkitut saavat mitalinsa.

Kaksi kilpailijaa ylsi maksimipistemäärään, toinen Yhdysvalloista ja toinen Iso-Britanniasta.

Kokonaisuutena parhaiten menestynyt maa on tänä vuonna Yhdysvallat. Toiseksi on yltänyt Venäjä, kolmanneksi Kiina. Lisäksi kärkikymmenikössä ovat Ukraina, Thaimaa, Taiwan, Etelä-Korea, Singapore, Puola ja Indonesia.

Järviniemi ja Honkamaa saavat pronssia, Jussinmäki ja Virtanen kunniamaininnat. Koko joukkueen sijoitus on 59. Se on paras tulos sitten vuoden 2006.

Päivitetty 13.10.2020 – Ilmestynyt 4.10.2018